Data is now the most valuable resource in the world. How should it be priced?
“This thing called ‘price’ is really, really important. I still think that a lot of people under-think it through. You have a lot of companies that start and the only difference between the ones that succeed and fail is that one figured out how to make money, because they were deep in thinking through the revenue, price, and business model. I think that’s under-attended to, generally.” – Steve Ballmer, Former CEO, Microsoft.
The business of monetizing data has grown significantly over the past decade and has created unprecedented opportunities for firms to market their products, advance their predictive abilities, and target customers with surgical precision. As proclaimed in The Economist, data is now the most valuable resource in the world. The growth in the value of data is primarily fueled by the intelligence that data-driven analytics provides in making critical business decisions. While there are a ton of articles in the popular press about the perks of monetizing data, little is known about how data should be actually priced. Motivated by the practical and theoretical significance of data monetization, we (my advisors and I) have developed a framework that is appropriate for the purchasing of data by a buyer and the corresponding pricing by the seller. In this article, I will briefly explain this framework and highlight the key findings of our research paper.
An initial challenge that any firm in the business of data monetization faces is to build an efficient data warehouse to integrate data from disparate sources. Even when a firm manages to put together a high-quality, uninferred, and well-structured dataset that complies with user-privacy—which can be a daunting task in its own right—appropriately pricing that dataset is crucial to the success of monetization. A dataset is essentially an information good. Its value is derived from the information that it contains. While economists have studied how to price information goods in general, the selling of a dataset, as I will explain below, is more nuanced than that of information goods like telephone minutes and internet bandwidth.
Consider the illustrative dataset on the mobile activity of smartphone users in North America shown in Table 1. Such a dataset is highly valuable for marketers as it helps them execute targeted campaigns. Moreover, the valuations for different subsets of records by different marketers vary; that is, the records of interest and the corresponding value for them differ across buyers. A natural question then arises: How should the data-seller price such a dataset? Should he specify a price for each potential set of records that a buyer can select? Clearly, it would be impractical to even specify such a set-based pricing policy due to its exponential size. Should he make a simple take-it-or-leave-it (A pricing policy in which the buyers are required to either purchase all the records in the dataset at a given price or buy nothing.) offer to the buyers? This, of course, would turn away a lot of buyers who are interested in purchasing only a few records (of their choice) from the dataset. To answer these questions, we develop a mathematical model with the following features:
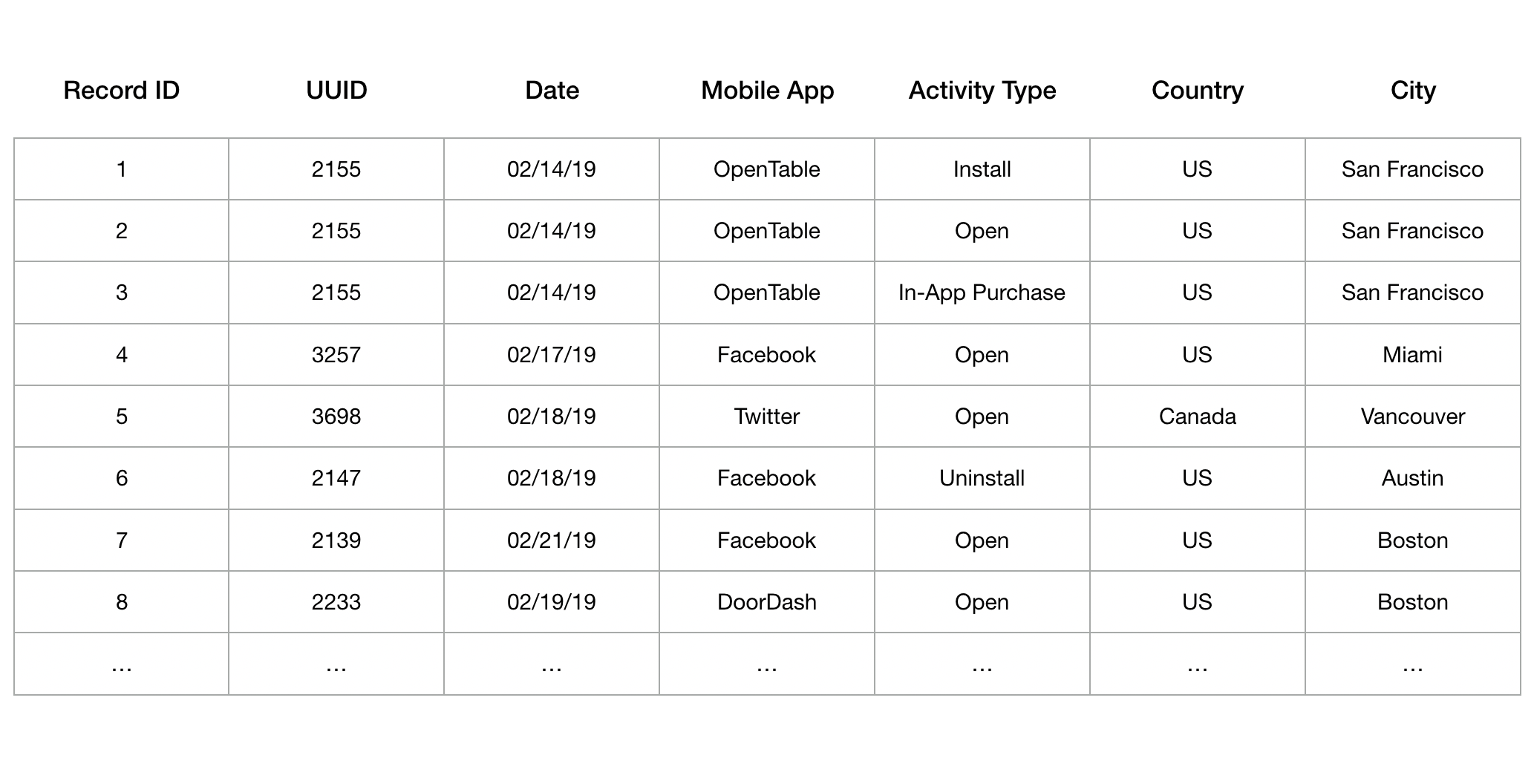
Table 1: An illustrative dataset consisting of information on mobile activity by smartphone users.
- Ideal record: Each buyer has an ideal record that she values the most. For instance, in the illustrative dataset shown in Table 1, an ideal record for a youth-apparel advertiser in California, might be that of a user who is based in San Francisco and has made an in-app purchase on the OpenTable app on Valentine’s day (Record ID 3). Similarly, a competitor of DoorDash might be interested in a user who used (opened) the DoorDash app in the Boston area in the last week (Record ID 8).
- Distance from the ideal record: We employ the notion of a distance metric to measure how close a specific record in the dataset is to a buyer’s ideal record – farther this distance, lesser is the buyer’s value for the record. The notion of distance is then used to rank order the records in the dataset for different buyers. Naturally, buyers prefer records that are closer to their respective ideal records.
- Decay rate: A number which determines the rate at which a buyer’s valuation for a record decays as its distance from the ideal record of that buyer increases.
- Filtering of records: An option (provided by the seller) through which individual buyers can select the records that are of interest to them. In the absence of filtering, the buyers would have to either purchase all the records in the dataset or buy nothing.
For each individual buyer, her ideal record and decay rate are her private information, which she uses along with the seller’s pricing policy to purchase the records of her choice. Anticipating the buyers’ decisions, the seller’s goal is to design a pricing policy that maximizes his expected revenue. The multi-dimensional private information of the buyers coupled with their endogenous selection of records makes the seller’s problem of optimally pricing the dataset a challenging one. I will now highlight the key results from our analysis.
- When the records in the dataset are “uniformly distributed”, we show that a price-quantity schedule is an optimal data-selling policy. Broadly speaking, the uniform distribution of records signifies that any two buyers with different ideal records find roughly the same number of records within a fixed distance from their respective ideal records. As the name suggests, under a price-quantity schedule, the seller sets a fixed price for a given number of records. Thus, the price depends only on the quantity of the records selected by a buyer and not on their identity. The significance of this result lies in the implication that in the search for an optimal pricing policy, the seller can restrict his attention to schedules in which price depends only on the number of records chosen by the buyer and not on the identity of those records.
- When the uniform distribution assumption does not hold, a price-quantity schedule may no longer be optimal. Nevertheless, in this case, the best price-quantity schedule performs reasonably well and yields provably near-optimal revenue. However, designing the best price- quantity schedule may not be straightforward and business needs dictate that pricing policies should be simple and easily understood. The good news is that simple price-quantity schedules, such as two-part tariffs and two-block tariffs, perform handsomely.
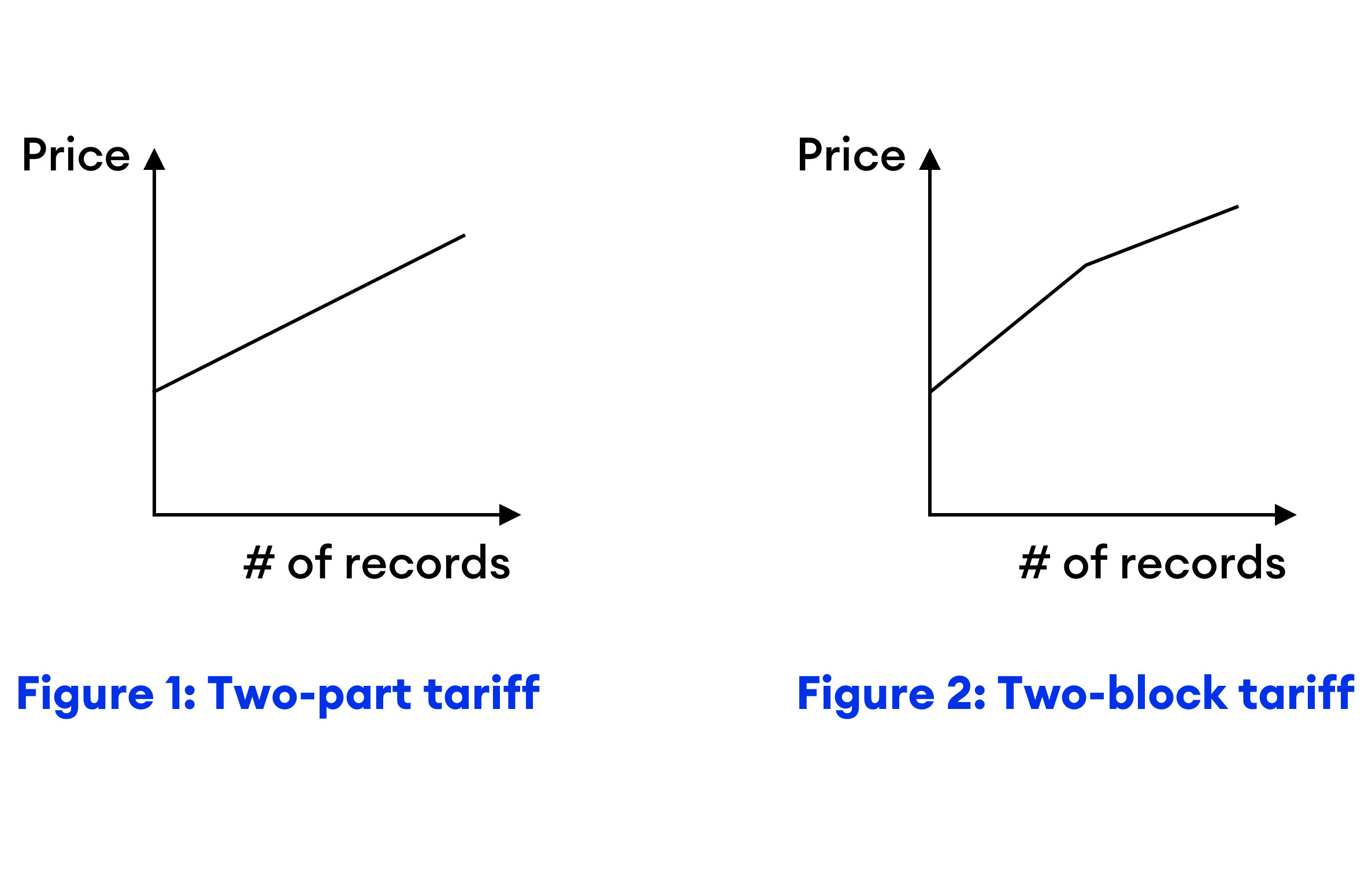
- Two-part tariff: As shown in Figure 1, a two-part pricing policy consists of two parts: a lump-sum (fixed) fee and a per-record (variable) price. For example: A lump-sum fee of $50 and a per-record price of $0.04.
- Two-block tariff: The two-block pricing policy is more general than the two-part policy. Under this policy, the seller charges a lump-sum fee and sets two per-record prices – one for low-quantity buyers and other for high-quantity buyers (see Figure 2). For example: A lump-sum fee of $20 and $0.05 per-record for the first 1000 records and $0.03 per-record for records in excess of 1000.
Interestingly, these simple pricing policies are able to achieve over 80% of the optimal revenue.
- In the final leg of our analysis, we quantify the value that accrues to the seller from allowing the buyers to filter data. This “value of filtering” to the seller depends on the fraction of records in the dataset that are valuable to the buyer: The lower this fraction, the more important it is for the buyer to use filtering to identify the desired set of records and, thus, higher is the value of filtering.
This research focused on a monopolistic data-seller who is interested in monetizing a dataset and is a first step towards understanding how datasets should be priced. The ongoing explosive growth in the supply and demand of data has led to the emergence of data-selling platforms, such as Narrative, that cater to both sides of the market: sellers list their datasets on the platform and buyers purchase data from one or more sellers. Such two-sided settings become richer due to several interesting constraints:
- On the supply-side, some sellers may want to sell their data only as a monolithic unit (i.e., avoid sale of proper subsets of records) and some may want to restrict sale to a limited number of buyers.
- On the demand-side, buyers may want exclusive access to data or may have budget and/or minimum-volume constraints.
Further, from a market-design perspective, the analysis of two-sided data-selling platforms presents interesting theoretical and practical challenges. For instance, the utility of a dataset to a buyer may depend on the number of other buyers who have shared access to that dataset. I believe that our current findings can serve as a foundation for future work on optimal and/or approximate mechanisms for such settings and, more generally, on the design of efficient data-selling platforms.



